We shall condense the visual processing of our nervous system in order to considering the foundation of geometry. The first stage of visual processing is the photoreceptor cell. When a photoreceptor cell absorbs photons, it changes membrane potential. As a result, the first image is 2D raster image in the retina. However, we are seeing the 3D vector image, which is the final product of our visual processing. Though there are many stages between them, Hubel and Wiesel found the key stage of the visual processing. It is the extraction of the edge in the primary visual cortex. At the stage, the raster image is converted into the vector image.
Receptive Field of the Simple Cells
Hubel and Wiesel had been investigated the visual processing of the animal's nervous system. They sought the most effective stimulus for the neuron of the primary visual cortex. Initially, they classified cells into simple cells and complex cells, and then they elucidated the receptive field of the simple cell (2)(3). They continued experiments (4), and then they received the Nobel Prize in 1981. Figure 1 shows three types of the receptive fields of simple cells.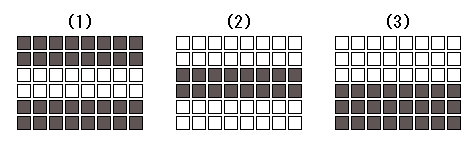
Figure1
Figure 1-1 shows the receptive field of the cell, which responds best to the light bar flanked by two dark areas. Figure 1-2 shows that of the cell, which responds best to the inverted pattern of figure 1-1. Figure 1-3 shows that of the cell, which responds best to the borderline between the light and dark areas. We shall focus on this type of the simple cell.
The Plane Geometry with Pixels
Above schemata are drastically simplified. However, they are enough in order to discuss the base of mathematics. If you want to know more in detail, please visit Hubel's website. Let us consider figure 1-3. The borderline corresponds to the edge of the 3D object. The edge is important to form the contour of the 3D object.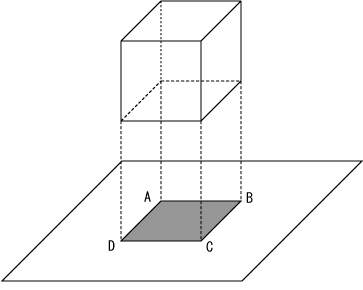
Figure2
>Figure 2 shows the shadow of the cube. The line AB is the borderline between the light and dark areas. Line AB is magnified in the next figure.
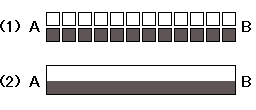
Figure3
Figure 3-1 shows the raster image of the line AB. There is no pixel on the line AB. That is, the line AB is not a substantial entity. Next, simple cells convert the raster image into the vector image. Figure 3-2 shows the vector image of the line AB. Euclid defines that a line is breadthless length: definition 2 of Book Ⅰ in the Elements. So, it has no width, and the length equals the number of pixels.
Next, a point has no width and no length. So, anyone cannot detect a sole point. In contrast, if a point is the end of line, we can detect it. Because points A and B are opposite ends of the line AB, we can detect them. So, Euclid defines that the ends of a line are points: definition 3 of Book Ⅰ in the Elements. Furthermore, we can obtain Euclidean straight lines of all directions and all orientations in the primary visual cortex.
Next, a point has no width and no length. So, anyone cannot detect a sole point. In contrast, if a point is the end of line, we can detect it. Because points A and B are opposite ends of the line AB, we can detect them. So, Euclid defines that the ends of a line are points: definition 3 of Book Ⅰ in the Elements. Furthermore, we can obtain Euclidean straight lines of all directions and all orientations in the primary visual cortex.
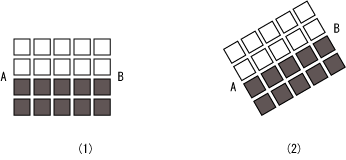
Figure4
Figure 4-1 shows one directional receptive field of the simple cell. Figure 4-2 shows another directional receptive field of the simple cell. These lines are converted into Euclidean straight lines.
Our built-in geometry is not the product based on the logical blue print but the product of the evolution, which is influenced accidentally. That is, it contains internal contradictions. It has both the pixel and the pseudo-Euclidean line. However, it is logically difficult to make the pixel and the true Euclidean line coexist. If we want to make the logical geometry, we have to choose either. Ideally, the ideal geometry must be based on the number theory. The pixel corresponds to the natural number one in principle. Hence, the ideal geometry must be constructed from pixels. Even so, ancient Greeks gave preference to the Euclidean line over the pixel. As a result, their Euclidean geometry is based on not the number theory but axioms. Why did they abandon pixels? Let us consider the reason.
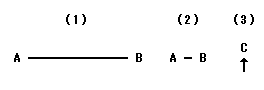
Figure5
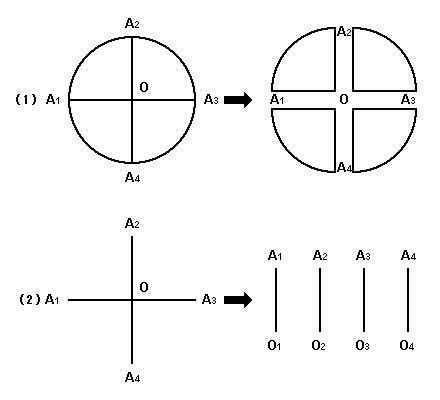
Figure6
Our Built-in Geometry
We obtain Euclidean straight lines in the primary visual cortex. So, the human brain has the built-in geometry. However, our built-in geometry is different from the true Euclidean geometry. Because our vector image is constructed from the retinal raster image, it cannot be true vector image. Our brain conceals pixels and show us pseudo-vector image. We feel as if we see true 3D vector image. However, the feeling is a kind of illusion. We are forcedly made to understand the fact in the eye test. Our visual image is vague, and we cannot recognize the shape of the figure in the distance. That is to say, our Euclidean line is the pseudo-Euclidean line. Hence, it becomes cloud in the distance. Therefore, the pseudo-vector image, which we are seeing, is made from pixels. Our built-in geometry has both the pseudo-Euclidean line and the pixel.Our built-in geometry is not the product based on the logical blue print but the product of the evolution, which is influenced accidentally. That is, it contains internal contradictions. It has both the pixel and the pseudo-Euclidean line. However, it is logically difficult to make the pixel and the true Euclidean line coexist. If we want to make the logical geometry, we have to choose either. Ideally, the ideal geometry must be based on the number theory. The pixel corresponds to the natural number one in principle. Hence, the ideal geometry must be constructed from pixels. Even so, ancient Greeks gave preference to the Euclidean line over the pixel. As a result, their Euclidean geometry is based on not the number theory but axioms. Why did they abandon pixels? Let us consider the reason.
The Line and the Point
Because ancient Greeks refine our pseudo-Euclidean line into the true Euclidean line, we shall consider the relationship between the line and the point. If there is no length between two points, they are the same point. That is, there must be a length between two different points. Then, we can draw a line between two different points.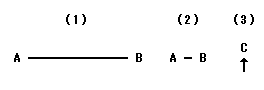
Figure5
Figure 5-1 shows the line AB. Points A and B are ends of the line AB. If there is a length between two points, they are different points. Figure 5-2 shows a short line between points A and B. If there is no length between points A and B, they are the same point. We shall call it the point C. Figure 5-3 shows only the location of the point C. Because it has no length and no width, we cannot see it. That is, the isolated point does not exist substantially. So, Euclid define point as the end of a line.
This means that an isolated point is not a substantial entity. Instead, two points are generated by a cut of a line. Furthermore, two lines are generated by a cut of an area (5). That is, areas correspond to pixels. In contrast, points and lines correspond to nothing. The area needs to exist beforehand, so that the point and the line can exist.
This means that an isolated point is not a substantial entity. Instead, two points are generated by a cut of a line. Furthermore, two lines are generated by a cut of an area (5). That is, areas correspond to pixels. In contrast, points and lines correspond to nothing. The area needs to exist beforehand, so that the point and the line can exist.

Figure6
The left side of figure 6-1 shows the circle in the Euclidean Plane. The point O is the center of the circle, and the line A1A3 and the line A2A4 are orthogonal at the point O. Let us cut the circle along these lines like cutting pizza. The right side of figure 6-1 shows the result, the center point is apparently a blank. This means that the center point is divisible without limit. That is, zero can be divided any number of times. Instead, no matter how many zero are collected, the total equals zero.
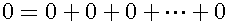
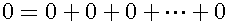
Next, the left side of figure 6-2 shows only two diameters. We shall cut them into four radii. Then, the point O is divided into points O1, O2, O3 and O4. That is, the total length of any number of points on the circumference equals the point O. No matter how many points are collected, we cannot obtain any length. In other word, a line doesn't consist of points.
This fact causes the next problem. A line cannot be defined as the collection of points. However, there are the circle, the ellipse and the parabola. If we want to draw these curves, we must determine the position of each point on the curve. That is, the curve is the collection of the points. Therefore, the true curve is the impossible figure.
As mentioned above, the Euclidean geometry cannot be constructive, and it contains contradictions. The ancient Greeks noticed this problem. Zeno of Elea stated the dichotomy paradox. He asserts the non-existence of motion. If our space is the Euclidean space, the movement is impossible. If we want to move to any point, we must arrive at the halfway. Before arriving at the halfway, we must arrive at 1/4 of the way. Before arriving at 1/4 of the way, we must arrive at 1/8 of the way; and so on.
The dichotomy paradox and the above fact are due to the same cause. That is, there isn't the adjacent point. Hence, the length is necessary between different two points. In other word, the line can exist between different two points. Furthermore, the line is the border of two pixels. Therefore, the pixel is necessary for the plane geometry. Because lines and points are blanks, the area cannot be constructed from them. So, the area must consist of pixels.
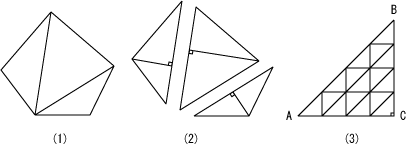
Figure7
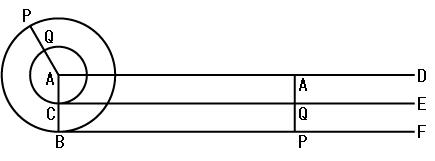
Figure8
Figure9
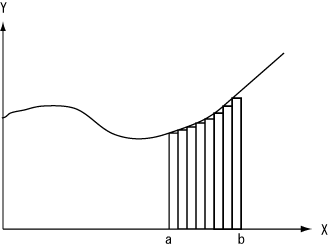
Figure10
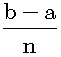
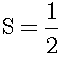

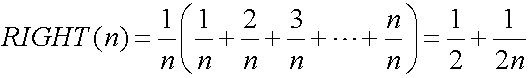
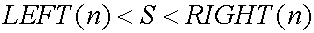
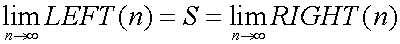

Figure12
This fact causes the next problem. A line cannot be defined as the collection of points. However, there are the circle, the ellipse and the parabola. If we want to draw these curves, we must determine the position of each point on the curve. That is, the curve is the collection of the points. Therefore, the true curve is the impossible figure.
As mentioned above, the Euclidean geometry cannot be constructive, and it contains contradictions. The ancient Greeks noticed this problem. Zeno of Elea stated the dichotomy paradox. He asserts the non-existence of motion. If our space is the Euclidean space, the movement is impossible. If we want to move to any point, we must arrive at the halfway. Before arriving at the halfway, we must arrive at 1/4 of the way. Before arriving at 1/4 of the way, we must arrive at 1/8 of the way; and so on.
The dichotomy paradox and the above fact are due to the same cause. That is, there isn't the adjacent point. Hence, the length is necessary between different two points. In other word, the line can exist between different two points. Furthermore, the line is the border of two pixels. Therefore, the pixel is necessary for the plane geometry. Because lines and points are blanks, the area cannot be constructed from them. So, the area must consist of pixels.
The Obstacles of the Geometry with Pixels
The human brain has the built-in geometry with pixels. It can represent the Euclidean straight line. Furthermore, it is sufficient for practical usage. Why did ancient Greeks abandon pixels? The time of Pythagoras, they tried to make geometry based on pixels. However, the first obstacle was the irrational magnitude. If the pixel is only the isometric regular polygon, the irrational magnitude cannot be obtained. However, I think that the atomic theory of Democritus was devised to overcome this difficulty. According to the atomic theory, atoms are indivisible, and there are infinite kinds of atoms, which differ in shape and size. Now, anyone doesn't know Democritus's geometry. Even so, let us conjugate his geometry. We shall apply the atomic theory to the plane geometry.
Figure7
Figure 7-1 shows that any polygon can be divided into triangles. Likewise, any triangle can be divided into two rectangular triangles. If we use the rectangular triangle as a pixel, we can easily calculate the area. So, we shall regard the rectangular triangle as the atom of the plane geometry. Then, we can obtain irrational magnitudes. Figure 7-3 shows the isosceles rectangular triangle ABC, which consists of isomorphic atoms. According to Pythagolean theorem, AC:BC:AB = 1:1:√2.
Next, atoms are indivisible pixels, which differ in shape and size. Furthermore, the plane geometry with atoms can represent any figures, which consist of straight lines. It is my tentative proposal of the geometry, which contains both the Euclidean straight line and atoms.
If we consider the figure, which consists of points, it cannot consist of atoms. I think that the archetype of such a figure is a circle. It is defined as the collection of points in the modern mathematics (1). Perhaps, Euclid might notice the difficulty. He defines the circle as follows. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another: definition 15 of Book Ⅰ in the Elements. It seems that he ingeniously avoids defining the circle as the collection of points. However, he uses all radii for defining the circumference. One end of radius is the center point and another end of it is a point on the circumference. De facto in fact, his definition of the circle uses points as ends of radii. Substantively, he defines the circle as the collection of points.
I think that the circle is the second obstacle for making the plane geometry based on pixels. It cannot be constructed from pixels, because the borderline of two pixels is consistently the straight line. Hence, Euclid might discard pixels, and then he created the Euclidean geometry.
Ancient Greeks had not know the method of calculating the length of the circumference for a long time. Finally, Archimedes approximated the value of Pi. However, he only approximated the circle by the polygon. That is, if we want to treat the curve quantitatively, we need to approximate it by straight lines. The method of the approximation is the calculus.
Archimedes is considered to be the founder of the integral calculus. However, its origin can be traced back to Democritus. Leslie William Gates says as follows:
Next, atoms are indivisible pixels, which differ in shape and size. Furthermore, the plane geometry with atoms can represent any figures, which consist of straight lines. It is my tentative proposal of the geometry, which contains both the Euclidean straight line and atoms.
If we consider the figure, which consists of points, it cannot consist of atoms. I think that the archetype of such a figure is a circle. It is defined as the collection of points in the modern mathematics (1). Perhaps, Euclid might notice the difficulty. He defines the circle as follows. A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure equal one another: definition 15 of Book Ⅰ in the Elements. It seems that he ingeniously avoids defining the circle as the collection of points. However, he uses all radii for defining the circumference. One end of radius is the center point and another end of it is a point on the circumference. De facto in fact, his definition of the circle uses points as ends of radii. Substantively, he defines the circle as the collection of points.
I think that the circle is the second obstacle for making the plane geometry based on pixels. It cannot be constructed from pixels, because the borderline of two pixels is consistently the straight line. Hence, Euclid might discard pixels, and then he created the Euclidean geometry.
Ancient Greeks had not know the method of calculating the length of the circumference for a long time. Finally, Archimedes approximated the value of Pi. However, he only approximated the circle by the polygon. That is, if we want to treat the curve quantitatively, we need to approximate it by straight lines. The method of the approximation is the calculus.
Archimedes is considered to be the founder of the integral calculus. However, its origin can be traced back to Democritus. Leslie William Gates says as follows:
According to Archimedes, Democritus applied the idea of atomism to geometry by using infinitesimals to find the formula for the volume of a cone. He was the first mathematician to give the formula for the volume of a pyramid – not just a square-based pyramid - but one whose base is a regular polygon with any number of sides, including the cone (which is just a circular-based pyramid).Therefore, the atomic theory is the premise of the integral calculus. At least, the precondition of the integral calculus is that the figure consists of indivisible elements.
The Galileo's Thought Experiment
If the size of the pixel was zero, the plane couldn't be constructed. If the complete circle exists, the size of the pixel must be zero. That is, the complete circle cannot exist anywhere. In other word, the complete circle is the impossible figure. In order to clarify more, we refer to Galileo's thought experiments (6).
Figure8
Figure 8 shows two concentric and rigidly connected circles. The large circle is twice as large as the small circle. Point A is the center of them. Points B and C are on their circumference. If the large circle makes one complete rotation along the line segment BF, the small circle also makes one complete rotation along the line segment CE. Simultaneously, the point A moves along the line segment AD. These three line segments are parallel and the length of them are equivalent. The first thought experiment shows that points on the circumference of the small circle are put into one-to-one correspondence with points on the large circle. However, the large circle is twice as large as the small circle. The problematic point of the first thought experiment is that the circle contact the line at only one point. Because the point is not a substantial entity, an arbitrary number of points can exist on any line. Thus, a length cannot consist of points. Furthermore, this thought experiment shows that the Euclidean geometry doesn't always suit the reality.

Figure9
Next, figure9 shows two concentric and rigidly connected squares. The large square is twice as large as the small square. If the large square makes one complete rotation along the horizontal line ABCDAB, the small suquare also makes one complete rotation. Firstly, the large square rotates about the point B until the line segment BC falls on the horizontal line. Simultaneously, line segment FG falls on line segment FG. Secondary, the large square rotates about the point C until the line segment CD fall on the horizontal line; and so on.
The second thought experiment shows that the perimeter of the small square does not traverse the same distance as the perimeter of the large square. A side of the small square corresponds to a side of the large square, and the ratio is one to two. Galileo says that this argument is applicable to all other polygons. If we consider the polygon with the great number of sides, we can obtain the good approximation of the circle. This model is better than the complete circle to simulate the real wheel. Because the circle is the impossible figure, cautions are required to use it as the model of the reality.
The second thought experiment shows that the perimeter of the small square does not traverse the same distance as the perimeter of the large square. A side of the small square corresponds to a side of the large square, and the ratio is one to two. Galileo says that this argument is applicable to all other polygons. If we consider the polygon with the great number of sides, we can obtain the good approximation of the circle. This model is better than the complete circle to simulate the real wheel. Because the circle is the impossible figure, cautions are required to use it as the model of the reality.
The Pixel and the Infinitesimal
Simple and complex cells in the primary visual cortex decompose the outline of a visual image into short line segments of various orientations (7). That is, our primary visual cortex extracts straight line segments. This means that curve is constructed in higher areas of the brain. Furthermore, the curve isn't compatible with the pixel. So, it is difficult for us to calculate an area enclosed by a curve. In order to solve the problem, mathematicians created integration. In the modern mathematics, the problem is reduced to calculate the area under the curve. We can approximate it by dividing it into rectangles and collecting them.
Figure10
Figure 10 shows an example of the approximation of the area under the curve in the interval between a and b. The narrower the width of the rectangle is, the better the accuracy of the approximation is. If we increase the number of rectangles towards infinity, the error of the approximation approaches zero. This is the idea of the definite integration. If the width of rectangles becomes zero, the area cannot be constructed from zero. So, it must not be zero. Inevitably, the concept of infinitesimal arises. That is, the width of rectangles becomes infinitesimal. However, the next question arises. What is infinitesimal?
Let us return to figure 9. When the area under the curve is divided into n rectangles. Then, the width of the rectangle is (b-a)/n:
Let us return to figure 9. When the area under the curve is divided into n rectangles. Then, the width of the rectangle is (b-a)/n:
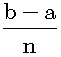
However, the width never reaches the infinitesimal. The proof by mathematical induction is as follows.
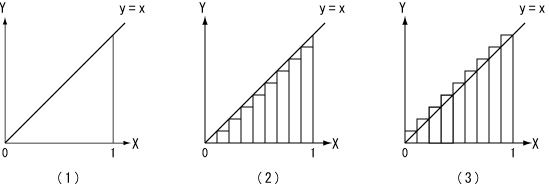
Figure11
Next, let us consider the area under the simple function y=x. Figure 11-1 shows the graph of y=x. We assume that the area under the line y=x in the interval [0,1] is S. S is easily calculated:
- (b-a)/1 is not the infinitesimal.
- If (b-a)/n is not the infinitesimal, then (b-a)/(n+1) is not the infinitesimal.
- So it is concluded that (b-a)/n never reaches the infinitesimal.

Figure11
Next, let us consider the area under the simple function y=x. Figure 11-1 shows the graph of y=x. We assume that the area under the line y=x in the interval [0,1] is S. S is easily calculated:
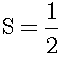
We shall calculate the area using the integral. Firstly, we divide interval [0,1] into n subintervals. Next, we choose the height of each rectangle as the value of the function at the left end point of each subinterval. In this case, the total area of rectangles is called the left sum. Figure 11-2 shows the left sum:

When we choose the right end point instead of the left end point, the right sum is obtained:
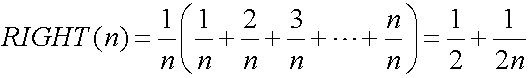
Because y=x is the monotonically increasing function, the next inequality is formed:
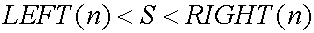
Using above inequality, we try to calculate S. However, the error 1/2n remains constantly. If we want to regard 1/2n as zero, we must assume the existence of pixels. If an area consists of pixels, there is the minimum length. So, when we choose sufficiently large n, 1/2n is smaller than the minimum length. Then we can regard 1/2n as zero. Therefore, the premise of the integration is the existence of pixels.
As n increases, the left sum and the right sum approaches S. We assume the difference between the value of them and S as ε.
As n increases, the left sum and the right sum approaches S. We assume the difference between the value of them and S as ε.
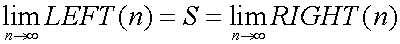
The left sum and the right sum converge the limit S. S is the area under the curve.
Next, let us consider the Euclidean line and the Euclidean geometry.
The Pixelated Geometry
Let us consider the meaning of the pixel. Firstly, our retinal image consist of pixels. We can get visual information only from our eyes. Secondly, if we draw a figure with a pencil, the point of it is the minimum dot. Even if we use any tool, there is the minimum pixel. Hence, we can draw only the raster image. Thirdly, our pseudo-vector image is only in our brain. That is, the geometries constructed from it can exist only in our brain. Therefore, they must be converted into the geometry based on identical pixels. We shall call it the pixelated geometry. Because the identical pixel corresponds to the natural number one, the pixelated geometry is compatible with the number theory (8). In order to maintain symmetry, the pixel must be the regular triangle or the regular tetragon or the regular hexagon. The point have the area and the line have the width. This geometry is different from the Euclidean geometry. However, because the Euclidean geometry is only in the brain, it must be converted into the pixelated geometry. Then, we can determine the size of the pixel depending on the intended use. Therefore, the pixelated geometry is sufficient for the practical usage.Next, let us consider the Euclidean line and the Euclidean geometry.

Figure12
Figure 12 shows the Landolt ring, which is used for eye test. It seems that the borderlines of the gap is Euclidean lines. However, we cannot recognize them in the distance. So, they consist of pixels. If we cannot detect any white pixel in the gap, we regard the Landolt ring as the black ring. That is, our Euclidean line is a illusion.
So, the pixel is the fundamental element of the geometry. Furthemore, the pixel is the contact point between the number theory and the geometry. However, Euclid discaded pixels. Inevitably, he had to construct geometry based on axioms. Even so, many defects occur by the lack of the pixel. Because there is not an adjacent point, an area and a line cannot be constructed from points. So, it is impssible to compose the length and the width. Furthermore, the meaning of the area is unclear.
Moreover, Euclid tried to define fundamental elements of geometry by the language. The trial had to fall into the circular reference. This is the fault of the language itself. For example, a word of a dictiory is defined by other words. If we continue pursuing the meaning of a word in dictionary, we will return to the original word finally. This problem cannot be fully solved. In contrast, the number theory has the biological foundation, because the natural number one is abstracted from a life (9). That is, the pixelated geometry can escape the circular reference.
Although the pixelated geometry is more rational, why ancinet Greeks created the Euclidean geometry? Their great discovery is the proof. Many proofs of theorems need the complete circle. It can exist in the Euclidean plane. This is the value of the existance of the Euclidean geometry. However, the human beings cannot reach the complete circle. Furthermore, the continuity arises many paradoxes. Especially, Zeno's paradoxes are famous. Because the Euclidean geometry was constructed from our vague visual image, it might have internal contradictions. Therefore, the Euclidean geometry must be coupled to the pixelated geometry.
At last, we shall consider the conversion of the Euclidean geometry into the pixelated geometry and the size of the exceedingly small magnitude. Whenever we recognize the real world, the minimum length certainly exists. For example, because the limit of the resolving power of our eyes is about 0.15 mm, which is the minimum length of our vision. Thereby, if we construct the pixelated geometry based on our vision, a side of the unit square is 0.15mm. Next example, the limit of the resolving power of the light microscope is about 0.2μm. In this case, if we construct the pixelated geometry, a side of unit square is 0.2μm. Thus, the minimum length changes with the detection device to be used. We can change the minimum length by selecting the detection device for the intended use. That is, the size of the pixel of the pixelated geometry is determined according to the intended purpose. Then, we regard the sufficiently smaller length than the pixel as the exceedingly small magnitude.
So, the pixel is the fundamental element of the geometry. Furthemore, the pixel is the contact point between the number theory and the geometry. However, Euclid discaded pixels. Inevitably, he had to construct geometry based on axioms. Even so, many defects occur by the lack of the pixel. Because there is not an adjacent point, an area and a line cannot be constructed from points. So, it is impssible to compose the length and the width. Furthermore, the meaning of the area is unclear.
Moreover, Euclid tried to define fundamental elements of geometry by the language. The trial had to fall into the circular reference. This is the fault of the language itself. For example, a word of a dictiory is defined by other words. If we continue pursuing the meaning of a word in dictionary, we will return to the original word finally. This problem cannot be fully solved. In contrast, the number theory has the biological foundation, because the natural number one is abstracted from a life (9). That is, the pixelated geometry can escape the circular reference.
Although the pixelated geometry is more rational, why ancinet Greeks created the Euclidean geometry? Their great discovery is the proof. Many proofs of theorems need the complete circle. It can exist in the Euclidean plane. This is the value of the existance of the Euclidean geometry. However, the human beings cannot reach the complete circle. Furthermore, the continuity arises many paradoxes. Especially, Zeno's paradoxes are famous. Because the Euclidean geometry was constructed from our vague visual image, it might have internal contradictions. Therefore, the Euclidean geometry must be coupled to the pixelated geometry.
At last, we shall consider the conversion of the Euclidean geometry into the pixelated geometry and the size of the exceedingly small magnitude. Whenever we recognize the real world, the minimum length certainly exists. For example, because the limit of the resolving power of our eyes is about 0.15 mm, which is the minimum length of our vision. Thereby, if we construct the pixelated geometry based on our vision, a side of the unit square is 0.15mm. Next example, the limit of the resolving power of the light microscope is about 0.2μm. In this case, if we construct the pixelated geometry, a side of unit square is 0.2μm. Thus, the minimum length changes with the detection device to be used. We can change the minimum length by selecting the detection device for the intended use. That is, the size of the pixel of the pixelated geometry is determined according to the intended purpose. Then, we regard the sufficiently smaller length than the pixel as the exceedingly small magnitude.
References
- The Foundations of Geometry
- Receptive fields of single neurones in the cat's striate cortex
- Transformation of Information in the cat's visual system
- Receptive fields and functional architecture of monkey striate cortex
- Area Is Essential for Euclidean Geometry
- Dialogue Concerning Two New Sciences
- Principles of Neural Science
- The Integration of Mathematics
- What Is the Natural Number One?